Giải toán 8 nhân đa thức với đa thức
Mục lục
Xem toàn cục tài liệu Lớp 8: trên đâyXem tổng thể tài liệu Lớp 8
: tại đâySách giải toán 8 bài bác 2: Nhân nhiều thức với đa thức giúp bạn giải những bài tập vào sách giáo khoa toán, học xuất sắc toán 8 sẽ giúp đỡ bạn rèn luyện kĩ năng suy luận hợp lý và phù hợp logic, hình thành kĩ năng vận dụng kết thức toán học tập vào đời sống với vào các môn học khác:
Trả lời thắc mắc Toán 8 Tập 1 bài 2 trang 7: Nhân đa thức xy – 1 với nhiều thức x3 – 2x – 6.Bạn đang xem: Giải toán 8 nhân đa thức với đa thức
Lời giải
( xy – 1).(x3 – 2x – 6) = xy.(x3 – 2x – 6) + (-1).(x3 – 2x – 6)
=
xy.x3 + xy.(-2x) + xy.(-6) + (-1).x3 + (-1).(-2x) + (-1).(-6)
=
x(1 + 3)y – x(1 + 1)y – 3xy – x3 + 2x + 6
= x4y-x2 y – 3xy – x3 + 2x + 6
= x4y – x3 – x2y – 3xy + 2x + 6
Trả lời câu hỏi Toán 8 Tập 1 bài 2 trang 7: có tác dụng tính nhân:a) (x + 3)(x2 + 3x – 5);
b) (xy – 1)(xy + 5).
Lời giải
a) (x + 3)(x2 + 3x – 5)
= x.(x2 + 3x – 5) + 3.(x2 + 3x – 5)
= x.x2 + x.3x + x.(–5) + 3.x2 + 3.3x + 3.(–5)
= x3 + 3x2 – 5x + 3x2 + 9x – 15
= x3 + (3x2 + 3x2) + (9x – 5x) – 15
= x3 + 6x2 + 4x – 15.
b) (xy – 1)(xy + 1)
= xy.(xy + 1) + (–1).(xy + 1)
= xy.xy + xy.1 + (–1).xy + (–1).1
= x2y2 + xy – xy – 1
= x2y2 – 1.
Trả lời thắc mắc Toán 8 Tập 1 bài bác 2 trang 7: Viết biểu thức tính diện tích s của một hình chữ nhật theo x và y, biết hai kích cỡ của hình chữ nhật đó là (2x + y) cùng (2x – y).Xem thêm: Top 10 Ứng Dụng Tạo Ảnh Hoạt Hình, Chuyển Ảnh Thật Thành Tranh Vẽ
Áp dụng: Tính diện tích hình chữ nhật khi x = 2,5 mét cùng y = 1 mét.
Lời giải
Biểu thức tính diện tích hình chữ nhật là:
S = (2x + y).(2x – y)
= 2x.(2x – y) + y.(2x – y)
= 2x.2x + 2x.(–y) + y.2x + y.(–y)
= 4x2 – 2xy + 2xy – y2
= 4x2 – y2
Áp dụng : lúc x = 2,5 mét cùng y = 1 mét
⇒ S = 4.2,52 – 12 = 4.6,25 – 1 = 25 – 1 = 24
Vậy diện tích s của hình chữ nhật là: 24 mét vuông
Bài 7 (trang 8 SGK Toán 8 Tập 1): có tác dụng tính nhâna) (x2 – 2x + 1)(x – 1)
b) (x3 – 2x2 + x – 1)(5- x)
Lời giải:
a) (x2 – 2x + 1)( x – 1)
= x2.(x – 1) + (–2x).(x – 1) + 1.(x – 1)
= x2.x + x2.(– 1) + (– 2x).x + (–2x).(–1) + 1.x + 1.(–1)
= x3 – x2 – 2x2 + 2x + x – 1
= x3 – (x2 + 2x2) + (2x + x) – 1
= x3 – 3x2 + 3x – 1
b) (x3 – 2x2 + x – 1)(5 – x)
= (x3 – 2x2 + x – 1).5 + (x3 – 2x2 + x – 1).(–x)
= x3.5 + (–2x2).5 + x.5 + (–1).5 + x3.(–x) + (–2x2).(–x) + x.(–x) + (–1).(–x)
= 5x3 – 10x2 + 5x – 5 – x4 + 2x3 – x2 + x
= –x4 + (5x3 + 2x3) – (10x2 + x2) + (5x + x) – 5
= –x4 + 7x3 – 11x2 + 6x – 5
Ta có:
(x3 – 2x2 + x – 1).(x – 5)
= (x3 – 2x2 + x – 1).<–(5 – x)>
= – (x3 – 2x2 + x – 1).(5 – x)
= – (–x4 + 7x3 – 11x2 + 6x – 5)
= x4 – 7x3 + 11x2 – 6x + 5.
Các bài bác giải Toán 8 bài xích 2 khác
Bài 8 (trang 8 SGK Toán 8 Tập 1): làm cho tính nhân: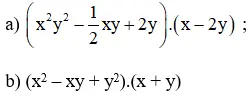
Lời giải:
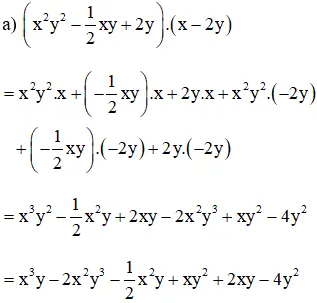
b) (x2 – xy + y2)(x + y)
= (x2 – xy + y2).x + (x2 – xy + y2).y
= x2.x + (–xy).x + y2.x + x2.y + (–xy).y + y2.y
= x3 – x2y + xy2 + x2y – xy2 + y3
= x3 + y3 + (xy2 – xy2) + (xy2 – xy2)
= x3 + y3
Các bài bác giải Toán 8 bài 2 khác
Bài 9 (trang 8 SGK Toán 8 Tập 1): Điền kết quả tính được vào bảng:| Giá trị của x cùng y | Giá trị biểu thức (x – y)(x2 + xy + y2) |
| x = -10 ; y = 2 | |
| x = -1 ; y = 0 | |
| x = 2 ; y = -1 | |
| x = -0,5 ; y = 1,25 |
Lời giải:
Ta có:
A = (x – y).(x2 + xy + y2)
= x.(x2 + xy + y2) + (–y).(x2 + xy + y2)
= x.x2 + x.xy + x.y2 + (–y).x2 + (–y).xy + (–y).y2
= x3 + x2y + xy2 – x2y – xy2 – y3
= x3 – y3 + (x2y – x2y) + (xy2 – xy2)
= x3 – y3.
Tại x = –10, y = 2 thì A = (–10)3 – 23 = –1000 – 8 = –1008
Tại x = –1 ; y = 0 thì A = (–1)3 – 03 = –1 – 0 = –1
Tại x = 2 ; y = –1 thì A = 23 – (–1)3 = 8 – (–1) = 9
Tại x = –0,5 ; y = 1,25 thì A = (–0,5)3 – 1,253 = –0,125 – 1,953125 = –2,078125
Vậy ta gồm bảng sau :
| Giá trị của x với y | Giá trị biểu thức (x – y)(x2 + xy + y2) |
| x = -10 ; y = 2 | -1008 |
| x = -1 ; y = 0 | -1 |
| x = 2 ; y = -1 | 9 |
| x = -0,5 ; y = 1,25 | -2,078125 |
Các bài xích giải Toán 8 bài bác 2 khác
Bài 10 (trang 8 SGK Toán 8 Tập 1): tiến hành phép tính :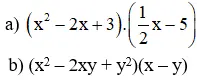
Lời giải:
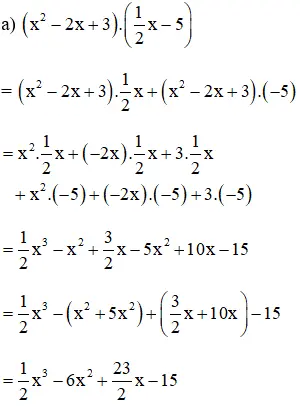
b) (x2 – 2xy + y2)(x – y)
= (x2 – 2xy + y2).x + (x2 – 2xy + y2).(–y)
= x2.x + (–2xy).x + y2.x + x2.(–y) + (–2xy).(–y) + y2.(–y)
= x3 – 2x2y + xy2 – x2y + 2xy2 – y3
= x3 – (2x2y + x2y) + (xy2 + 2xy2) – y3
= x3 – 3x2y + 3xy2 – y3.
Các bài bác giải Toán 8 bài 2 khác
Bài 11 (trang 8 SGK Toán 8 Tập 1): minh chứng rằng quý hiếm của biểu thức sau không nhờ vào vào quý hiếm của biến: (x – 5)(2x + 3) – 2x(x – 3) + x + 7Lời giải:
(x – 5)(2x + 3) – 2x(x – 3) + x + 7
= x.(2x + 3) + (–5).(2x + 3) – 2x.(x – 3) + x + 7
= (x.2x + x.3) + (–5).2x + (–5).3 – (2x.x + 2x.(–3)) + x + 7
= 2x2 + 3x – 10x – 15 – 2x2 + 6x + x + 7
= (2x2 – 2x2) + (3x – 10x + 6x + x) + 7 – 15
= – 8
Vậy với mọi giá trị của biến x, biểu thức luôn luôn có giá trị bằng –8
Các bài bác giải Toán 8 bài xích 2 khác
Bài 12 (trang 8 SGK Toán 8 Tập 1): Tính giá trị của biểu thức (x2 – 5)(x + 3) + (x + 4)(x – x2) trong mỗi trường đúng theo sau:a) x = 0 ; b) x = 15 ; c) x = -15 ; d) x = 0,15
Lời giải:
Rút gọn gàng biểu thức:
A = (x2 – 5)(x + 3) + (x + 4)(x – x2)
= x2.(x + 3) + (–5).(x + 3) + x.(x – x2) + 4.(x – x2)
= x2.x + x2.3 + (–5).x + (–5).3 + x.x + x.(–x2) + 4.x + 4.(–x2)
= x3 + 3x2 – 5x – 15 + x2 – x3 + 4x – 4x2
= (x3 – x3) + (3x2 + x2 – 4x2) + (4x – 5x) – 15
= –x – 15.
a) giả dụ x = 0 thì A = –0 – 15 = –15
b) giả dụ x = 15 thì A = –15 – 15 = –30
c) nếu như x = –15 thì A = –(–15) – 15 = 15 – 15 = 0
d) ví như x = 0,15 thì A = –0,15 – 15 = –15,15
Các bài bác giải Toán 8 bài xích 2 khác
Bài 13 (trang 9 SGK Toán 8 Tập 1): tra cứu x, biết:(12x – 5)(4x – 1) + (3x – 7)(1 – 16x) = 81
Lời giải:
Rút gọn gàng vế trái:
VT = (12x – 5)(4x – 1) + (3x – 7)(1 – 16x)
= 12x.(4x – 1) + (–5).(4x – 1) + 3x.(1 – 16x) + (–7).(1 – 16x)
= 12x.4x+ 12x.(–1) + (–5).4x + (–5).(–1) + 3x.1 + 3x.(–16x) + (–7).1 + (–7).(–16x)
= 48×2 – 12x – 20x + 5 + 3x – 48×2 – 7 + 112x
= (48×2 – 48×2) + (– 12x – 20x + 3x + 112x) + (5 – 7)
= 83x – 2
Vậy ta có:
83x – 2 = 81
83x = 81 + 2
83x = 83
x = 83 : 83
x = 1.
Các bài bác giải Toán 8 bài xích 2 khác
Bài 14 (trang 9 SGK Toán 8 Tập 1): Tìm tía số thoải mái và tự nhiên chẵn liên tiếp, biết tích của nhì số sau to hơn tích của nhị số đầu là 192.Lời giải:
