Công thức tính cấp số nhân
Cấp số nhân là một trong những dãy số (hữu hạn hoặc vô hạn).
Bạn đang xem: Công thức tính cấp số nhân
Trong đó kể từ số hạng sản phẩm 2, từng số hạn đông đảo là tích của số hạng đứng ngay trước nó cùng với số không thay đổi q. Số q hotline là công bội của cấp cho số nhânCông bội q
Gọi q là công bội của cấp số nhân ta có công thức công bội
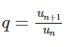
Ví dụ cho cấp số nhân (un) tất cả u1 = 2 , u2 = 4. Tính công bội q
Áp dụng bí quyết công bội q ta có
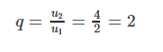
Nếu (un) là cấp số nhân với công bội q, ta tất cả un +1 = un.q, với mọi số nguyên dương n.
Tính hóa học của cung cấp số nhân
Định lí 1: nếu như (un) là 1 cấp số nhân thì tính từ lúc số hạng thứ hai, bình phương của mỗi số hạng (trừ số hạng cuối so với cấp số nhân hữu hạn) bằng tích của hai số hạng đứng kề nó vào dãy, tức là
u2k = uk-1 . Uk+1
Ví dụ: Cho cung cấp số nhân (un) cùng với công trét q > 0. Biết u1 = 1, u3 = 3. Hãy tìm kiếm u4
Giải:
Theo gắn lý 1 ta có
u22 = u1.u3
u32 = u2.u4
Từ (1) do u2 > 0 ( vì chưng u1 = 1 >0 cùng q > 0)
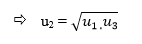
Từ đây và (2) ta được
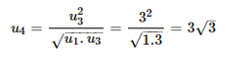
Số hạng tổng quát của cấp cho số nhân
Nếu một cấp cho số nhân bao gồm số hạng đầu (un) và công bội q thì số hạng tổng quát (un) sẽ tiến hành tính vày công thức:
un = u1. Qn-1
Ví dụ: Cho cấp số nhân un cùng với u1 = 3, q = -1/2. Search u7
Giải:
un = u1.qn-1 suy ra u7 = u1.q7-1 = 3 . (-1/2)6 = (3/64)
Tìm tổng n số hạng thứ nhất của một cấp cho số nhân
Giả sử bao gồm cấp số nhân (un) với công bội q. Với từng số nguyên dương n call sn là tổng n số hạng thứ nhất của nó. Ta co công thức sau
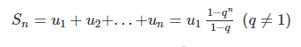
Nếu q = 1 thì cung cấp số nhân là sn = n.u1
Tổng của cung cấp số nhân lùi vô hạn
Cho cấp cho số nhân lùi vô hạn (un) có công bội là q. Lúc đó ta có tổng của cung cấp số nhân lùi vô hạn s bằng:
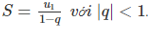
Ví dụ minh họa
Cho tía số a, b, c lập thành một cấp số nhân. Chứng minh rằng (a2 + b2) .
Xem thêm: Hình Nền Tên Người Yêu - Bật Hoặc Tắt Chế Độ Tập Trung Trên Iphone
(b2 + c2) = (ab + bc)2Ba số a, b, c lập thành một cấp cho số nhân ta được ac = b2
Khi: (a2 + b2) . (b2 + c2) = a2b2 + a2c2 + b4 + b2c2 = a2b2 + acb2 + b2c2 = a2b2 + 2ab2c + b2c2 = (ab + bc)2
Như vậy (a2 + b2) . (b2 + c2) = (ab + bc)2
Ví dụ 2: Tính tổng cung cấp số nhân S = 2 + 6 + 18 + … + 13122
Giải:
Xét cấp số nhân (un) có u1 = 2 với công bội q = 3
Ta tất cả :
13122 = un = unqn-1 = 2.3n-1 => n = 9
Như vậy suy ra
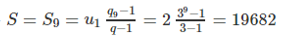
Ví dụ 3: search x để cha số x – 2, x – 4, x + 2 lập thành một cấp số nhân
Giải:
Để 3 x – 2, x – 4, x + 2 lập thành một cung cấp số nhân đk sẽ là
( x – 4 )2 = ( x – 2 ) ( x +2 ) => 8x = 20 => x = 5/2
Vậy x = 5/2 là số bắt buộc tìm để bố số x – 2, x – 4, x + 2 lập thành một cấp cho số nhân
BÀI TẬP RÈN LUYỆN VỀ CẤP SỐ NHÂNBài tập 1: minh chứng các dãy số sau là những cấp số nhân
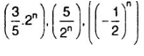
Giải:
Xét hàng số
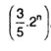
Lập tỉ số ( un+1 / un ) ta được :
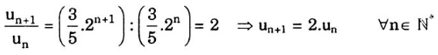
Suy ra dãy số bên trên là cấp cho số nhân tất cả công bội q = 2
Xét dãy số
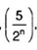
Lập tỉ số ( un+1 / un ) ta được :
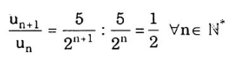
Suy ra (un) là cấp số nhân tất cả công bội q = ½
Xét dãy số
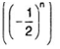
Lập tỉ số ( un+1 / un ) ta được :
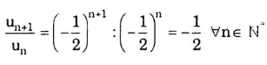
Suy ra (un) là cấp cho số nhân gồm công bội q = -½
Bài tập 2: Cho cấp số nhân (un) cùng với công bội q
a) Biết u1 = 2, u6 = 486. Search q
b) Biết q = 2/3, u4 = 8/21. Tra cứu u1
c) Biết u1 = 3, q = -2. Hỏi số 192 là số hạng lắp thêm mấy ?
Giải:
Áp dụng bí quyết un = u1. Qn-1
a) Theo công thức un = u1. Qn-1 ta có: u6 = u1.q5 => q5 = u6 / u1 = 486 / 2 = 243 => q = 3
b) Theo cách làm un = u1. Qn-1 ta có: u4 = u1.q3 => u1 = u4 / quận 3 = 8/21 . (3/2)2 = 9/7
c) Theo cách làm un = u1. Qn-1 ta có: 12 = 3. (-2)n-1 => (-2)n-1 = 64 => n-1 = 6 => n = 7 vậy nên 192 chính là số hạng đồ vật 7
Bài tập 3: Tìm những số hạng của cung cấp số nhân (un) bao gồm 5 số hạng biết:
a) u3 = 3 và u5 = 27
b) u4– u2 = 25 cùng u3 – u1 = 50
Giải:
Áp dụng bí quyết un = u1. Qn-1
a) Theo bí quyết un = u1. Qn-1 ta có
u3 = u1.q2 => 3 = u1.q2 (1)
u5 = u1.q4 => 27 = u1.q4 (2)
Từ (1) cùng (2) suy ra : q.2 = (u1.q4) / (u1.q2) = 9 => q = 3 hoặc -3
Với q = 3 ta được u1 = 1/3, ta gồm cấp số nhân là 1/3, 1, 3, 9, 27
Với q = -3 ta được u1 = 1/3, ta tất cả cấp số nhân là 1/3, -1, 3, -9, 27
b) Theo bài cho ta có :
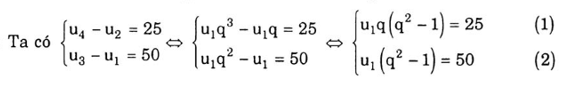
Thay (2) vào (1) ta được 50.q = 25 => q = ½
Từ (2) suy ra u1 = 50/(q2 – 1) = 50 / (1/4 – 1) = (-200 / 3)
Ta gồm cấp số nhân :
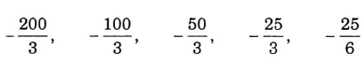
Bài tập 4 : Tìm cung cấp số nhân gồm sáu số hạng, biết rằng tổng của 5 số hạng đầu là 31 với tổng của 5 số hạng sau là 62
Giải :
Tổng của 5 số hạng đầu là 31 như vậy
u1 + u2 + u3 + u4 + u5 = 31
=> u1q + u2q + u3q + u4q + u5q =31q
=> u2 + u3 + u4 =+ u5 + u6 = 31q (1)
Tổng của 5 số hạng sau là 62 như vậy
u2 + u3 + u4 =+ u5 + u6 = 62 (2)
Từ (1) và (2) ta suy ra 31q = 62 => q = 2
Vì S5 = 31 = u1(1-25) / (1-2) => u1 = 1
Vậy ta được cấp cho số nhân : 1, 2, 4, 8, 16, 32
Bài tập 5: tỉ lệ thành phần tăng số lượng dân sinh của tỉnh x là 1,4%. Hiểu được số daancuar tỉnh bây chừ là 1,8 triệu người, hỏi với mức tăng lương do vậy thì sau 5 năm, 10 năm số dân của tỉnh kia là từng nào ?











